Posts Tagged ‘ CFD ’

Solusi Persamaan Diskrit

Persamaan – persamaan hasil diskritisasi volume untuk perhitungan numeric, seperti pada gambar 1, dapat diselesaikan dengan berbagai metode. Metode – metode apapun yang digunakan, pada prinsipnya, dapat menyelesaikan persamaan – persamaan ini untuk mencari solusi dari sistem persamaannya sendiri. Namun, untuk perhitungan – perhitungan yang rumit dengan jumlah persamaan dan variable yang banyak, dimana computer digunakan, algoritma kalkulasi yang efisien serta bersahabat dengan performa computer yang ekonomis perlu untuk dipahami.

Secara umum, metode yang digunakan adalah metode langsung (Direct) dan tidak langsung (Indirect atau Iterative). Yang dimaksud dengan metode langsung adalah suatu metode analitis yang digunakan langsung untuk mencari solusi dari sistem persamaan, contohnya adalah metode aturan cramer dan eliminasi Gauss. Pada metode ini, jumlah operasi perhitungan yang dilakukan dapat diketahui sebelumnya, yaitu, untuk menyelesaikan sebanyak N persamaan dengan N variable yang tidak diketahui, diperlukan N3 operasi dimana sebanyak N2 koefisien harus disimpan pada memori computer.

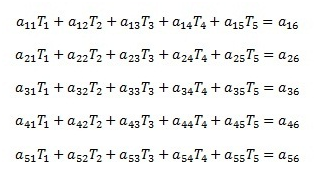Gambar 1. Contoh sistem persamaan linear

Tentunya, hal ini menjadi suatu hambatan tersendiri jika kemampuan computer yang akan digunakan mempunyai performa yang minim pada saat ingin dilakukan komputasi mengenai permasalahan, yang pada saat sudah didiskritisasi, membentuk suatu sistem persamaan dengan jumlah persamaan dan jumlah variable yang banyak sehingga akan diperlukan memori computer yang besar untuk menyimpan N2 koefisien.

Sedangkan metode tidak langsung atau iterative, merupakan metode yang berbasiskan terhadap aplikasi dari langkah – langkah/algoritma sederhana yang diulang – ulang pada sistem persamaan tersebut hingga sistem persamaan mencapai keadaan konvergen yang merepresentasikan solusi dari sistem persamaan tersebut. Pada metode iterative, banyaknya langkah – langkah perhitungan yang dilakukan tidak dapat diprediksi, dimana tipikalnya adalah sebanyak N perhitungan per satu kali iterasi. Kekurangan lainnya adalah, jika sistem persamaan tidak berada pada kondisi yang kondusif, maka konvergensi dari suatu sistem persamaan tidak dapat terjamin. Satu – satunya kelebihan dari penggunaan metode iterative adalah sedikitnya memori computer yang digunakan sebagai akibat dari algoritma yang mendesain agar computer hanya menyimpan koefisien – koefisien yang tidak nol. Simulasi – simulasi aliran fluida dapat memiliki jumlah persamaan dan variabel yang sangat banyak, mulai dari 1000 – 2 juta persamaan, yang tentunya dari sistem persamaan tersebut akan terdapat koefisien – koefisien nol, yang jika tidak disimpan pada memori computer, akan menghemat banyak ruang untuk performa computer.

Dikarenakan sistem persamaan Jacobi dan Gauss – Siedel yang lambat mencapai konvergensi pada saat sistem persamaan yang ditinjau mempunyai jumlah persamaan dan variable yang banyak, maka metode ini tidak digunakan pada prosedur kalkulasi CFD. Metode iterative selain Jacobi dan Gauss – Siedel, metode lain yang dapat digunakan adalah kalkulasi dengan menggunakan algoritma matrix tri – diagonal (TDMA) yang diperkenalkan oleh Thomas pada tahun 1949.

Tri – Diagonal Matrix Algorithm (TDMA)

TDMA merupakan metode kalkulasi iterative untuk komputasi CFD dua atau tiga dimensi dan merupakan algoritma standar untuk kalkulasi solusi persamaan aliran pada koordinat cartesius. Dapat diperhatikan salah satu contoh matriks tri – diagonal pada gambar 2.

Gambar 2. Contoh sistem persamaan yang membentuk matriks tri – diagonal

Pada gambar di atas, ϕ1 dan ϕn+1 adalah merupakan nilai batas yang diketahui. Bentuk umum dari setiap persamaan adalah seperti berikut,

Persamaan – persamaan pada gambar 2 dapat di atur ulang seperti berikut,

Gambar 3.

Untuk mendapatkan solusi terhadap ϕ, langkah kalkulasi yang pertama dilakukan adalah forward elimination dengan kemudian dilakukan back substitution untuk mendapatkan nilai – nilai ϕ. Inti dari forward elimination adalah mengatur ulang persamaan – persamaan pada gambar di atas. Dapat diperhatikan urutannya seperti pada gambar 4 untuk contoh forward elimination untuk ϕ3. Untuk langkah pertama, ϕ2 disubtitusi dari persamaan pertama seperti pada gambar 3 di atas.

Gambar 4. Forward Elimination  pada ϕ3

Setelah langkah pada gambar 4 diteruskan sampai ϕn, langkah back substitution dilakukan untuk kalkulasi solusi terhadap nilai – nilai ϕ. Dengan Back Substitution adalah langkah yang mencari solusi variable dari persamaan yang terakhir, dengan kemudian mensubtitusi persamaan terakhir tersebut ke persamaan sebelumnya, langkah ini terus dilakukan hingga nilai semua variable diperoleh.

Aplikasi TDMA

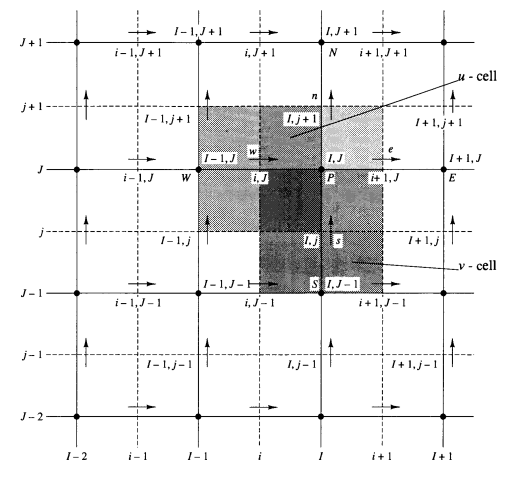
Pada kasus dua dimensi (lihat gambar 5), TDMA akan dilakukan dengan mengkalkulasi sistem persamaan pada satu arah dengan kemudian berpindah ke garis lainnya. Untuk lebih jelasnya, misal akan dilakukan suatu kalkulasi pada bidang dua dimensi seperti pada gambar 5, maka perlu dibuat sistem persamaan dari 1 sampai titik n. Setelah kalkulasi dari titik satu sampai titik n selesai, kalkulasi berpindah ke samping dengan arah yang sama dengan kalkulasi sebelumnya.

Gambar 5. Bidang dua dimensi

Misal, pada titik 2, persamaan yang terbentuk dapat berupa seperti pada gambar di bawah ini.

Gambar 6.

Untuk menyesuaikannya seperti persamaan pada gambar 2, maka persamaan di atas diatur seperti di bawah ini.

Gambar 7.

Dengan subskrip S, N, W, E, P adalah masing – masing koefisien dan variable sebelah selatan titik, koefisien dan variable sebelah utara titik, koefisien dan variable sebelah barat titik, koefisien dan variable sebelah timur titik, dan titik yang bersangkutan, serta b yang adalah suku sumber atau factor yang berkontribusi terhadap perubahan nilai – nilai atau distribusi variable ϕ pada daerah komputasi. Karena perhitungan bergerak dari selatan ke utara, maka nilai – nilai yang bersangkutan dengan titik sebelah barat dan sebelah timur titik yang bersangkutan dianggap diketahui (biasanya diberikan nilai nol). Begitu terus perhitungan dilakukan hingga variable – variable ϕ di setiap titik pada bidang diperoleh. Setelah itu, perhitungan dilakukan lagi (diulang/iterasi) hingga error terhadap solusi dari sistem persamaan mencapai toleransi yang telah ditetapkan sebelumnya.

Sedangkan untuk kasus tiga dimensi, perhitungan pada dasarnya sama seperti pada kasus dua dimensi. Namun, sebelum kalkulasi sistem persamaan diiterasi, pergerakan perhitungan bergerak ke atas/ bawah terlebih dahulu untuk mendapatkan variable pada semua daerah komputasi. Berikut contoh gambar untuk memperjelas aplikasi TDMA pada kasus tiga dimensi.

Gambar 8. Daerah komputasi tiga dimensi

Serta berikut contoh persamaan pada setiap titik di kasus komputasi tiga dimensi.

Untuk contoh kalkulasi pada model fisikanya, referensi versteeg [1] dapat menjadi bahan acuan. Sedangkan beberapa contoh – contoh kalkulasi iterasi dapat diperhatikan pada Metoda Iterative Bisection dalam kalkulasi solusi persamaan polynomial orde tiga, Kalkulasi ketinggian cairan pada tanki horizontal dengan menggunakan Microsoft Visual Basic. Serta berikut pembahasan  – pembahasan singkat mengenai kalkulasi solusi sistem persamaan, Kalkulasi solusi persamaan aljabar simultan, Metoda Iterasi.

Referensi:

[1] HK Versteeg. Malalasekera W. An Introduction to Computational Fluid Dynamic : Chapter 7. Longman Scientific and Technical. 1995.

2012
05/21
CATEGORY
Computational Fluid Dynamic
Komputasi Teknik
TAGS









Tinggalkan komentar

Grid Sensitivity Study

Diskritisasi volume yang dilakukan pada perhitungan numerik memerlukan pemilihan ukuran yang optimal berdasarkan sudut pandang ekonomi dan teknis. Yang dimaksud dengan sudut pandang ekonomi di sini adalah lamanya waktu perhitungan. Lamanya waktu perhitungan yang dilakukan pada perhitungan numerik merupakan dampak dari diskritisas volume itu sendiri di samping kemampuan/performa kalkulasi komputer yang digunakan. Semakin kecil volume – volume diskrit yang ditetapkan, maka akan semakin lama waktu perhitungan yang diperlukan, dimana kecilnya diskritisasi volume yang dilakukan proporsional dengan keakuratan hasil perhtungan. Dengan demikian, dapat diambil kesimpulan bahwa semakin kecil volume diskrit maka akan semakin lama waktu perhitungan dan akan semakin akurat hasil perhitunga, yang dimana hal ini mengatakan secara tidak langsung bahwa lamanya waktu perhitungan berbanding lurus dengan keakuratan hasil perhitungan.

Singkat kata, dalam studi sensitivitas grid, dilakukan suatu simulasi secara simultan dengan memvariasikan ukuran grid untuk mencari ukuran volume diskrit yang menghasilkan hasil perhitungan yang seakurat mungkin dalam waktu perhitungan yang sekecil mungkin.

Misal, akan dilakukan suatu studi terhadap pengaruh pengaruh ketajaman nosel terhadap kecepatan aliran fluida, dengan variasi sudut nosel 10, 20, 30, 50, dan 60 derajat. Maka perlu untuk terlebih dahulu melakukan grid sensitivity studi sebelum simulasi dilakukan untuk semua variasi sudut nosel. Misal grid sensitivity study dilakukan pada sudut nosel sebesar 60 derajat, dengan variasi grid sebesar 1, 0.5, dan 0.1 mm. Berdasarkan hasil simulasi studi sensitivitas grid, akan dilihat hasil kalkulasinya yang, misal, merepresentasikan kecepatan fluida. Berdasarkan hasil simulasi ini, akan diperhatikan daerah – daerah yang memiliki perbedan nilai. Misal antara grid 1, 0.5, dan 0.1 mm, perbedaan yang paling mencolok terhadap kecepatan fluida terdapat pada aliran fluida di dekat nosel, maka perlu untuk memperkecil ukuran grid pada daerah nosel, namun jika grid 1 mm sudah cukup akurat untuk daerah selain daerah pada nosel (ditandakan dengan tidak adanya perbedaan yang berarti untuk kecepatan fluida di daerah selain nosel pada ukuran grid 1, 0.5 dan 0.1 mm) maka grid 1 mm kiranya perlu untuk dialokasikan untuk memperkecil waktu perhitungan (berdasarkan sudut pandang ekonomi). Dari penjelasan di atas, maka dapat diambil kesimpulan bahwa ukuran grid yang kecil perlu untuk ditetapkan pada daerah – daerah yang mempunyai kontribusi yang berarti untuk menyebabkan kondisi aliran fluida berubah. Beberapa  contoh – contoh kondisi yang perlu untuk diperkecil ukuran gridnya (keakuratan perhitungannya) adalah daerah reaksi (misal pembakaran), sambungan reduksi, katup, aliran bluff body, dan masih banyak lagi.

Berikut ini akan ditampilkan hasil simulasi dua dimensi aliran di antara dua plat sejajar dengan variasi jumlah grid 50×50, 70×70, 90×90, 100×100, 120×120, 140×140. Berikut contoh geometri grid pada distribusi grid sebanyak 50×50.

Gambar 1. Distribusi grid 50×50

Boundary Layer Development

Berikut akan ditampilkan perubahan perubahan profil kecepatan pada daerah masukan relatif terhadap dua plat sejajar. Kita ketahui bersama bahwan pada daerah ini akan terjadi perkembangan boundary layer, maka dapat diambil kesimpulan bahwa daerah ini berkontribusi terhadap perubahan kondisi aliran fluida. Perubahan ini dapat diperhatikan secara berunut dari gambar 2 sampai gambar 7, dimana profil ini diambil dari sel i ke 1 sampai sel i ke 7.

Gambar 2. Boundary Layer Development pada grid 50×50

Gambar 3. Boundary Layer Development pada grid 70×70

Gambar 4. Boundary Layer Development pada grid 90×90

Gambar 5. Boundary Layer Development pada grid 100×100

Gambar 6. Boundary Layer Development pada grid 120×120

Gambar 7. Boundary Layer Development pada grid 140×140

Dari gambar 2 sampai gambar 7 di atas, dapat diambil kesimpulan bahwa dengan semakin akuratnya grid yang digunakan maka semakin menunjukkan perkembangan boundary layer yang akurat. Hal ini ditunjukkan dengan perbedaan – perbedaan yang terdapat pada gambar – gambar di atas. Namun, dengan pengamatan yang lebih lanjut lagi, dapat diperhatikan bahwa perkembangan boundary layer tidak begitu berbeda antara distribusi grid 120×120 dan 140×140. Dengan demikian, pada bagian masukan aliran di antara dua plat sejajar, distribusi grid sebesar 120×120 kiranya cukup untuk ditetapkan.

Profil Kecepatan

Profil kecepatan sepanjang arah aliran juga perlu untuk diperhatikan. Berikut akan ditampilkan profil kecepatan sepanjang arah aliran di pertengahan dua plat. Perubahan kondisi aliran berdasarkan variasi distribusi grid dapat diperhatikan pada fambar 8 sampai gambar 13.

Gambar 8. Profil kecepatan pada distribusi grid 50×50

Gambar 9. Profil kecepatan pada distribusi grid 90×90

Gambar 10. Profil kecepatan pada distribusi grid 90×90

Gambar 11. Profil kecepatan pada distribusi grid 100×100

Gambar 12. Profil kecepatan pada distribusi grid 120×120

Gambar 13. Profil kecepatan pada distribusi grid 140×140

Dapat diperhatikan pada gambar – gambar di atas secara berurutan bahwa kecepatan sepanjang arah x berubah di antara rentang 13 m/s sampai 11 m/s, khususnya pada daerah di dekat aliran masuk. Namun, dapat diperhatikan bahwa sekali lagi, bahwa sebagian besar kondisi aliran tidak berubah berdasarkan variasi distribusi grid pada daerah selain daerah masukan aliran. Pada daerah aliran masuk, perubahan yang tidak terlalu berbeda terdapat antara distribusi grid 120×120 dan 140, dengan demikian, kiranya dapat dialokasikan ukruran grid yang tidak uniform dimana pada daerah aliran masuk dan daerah seterusnya, masing  – masing, ditetapkan distribusi grid sebesar 120×120 dan 50×50.

2012
05/20
CATEGORY
Computational Fluid Dynamic
TAGS







Tinggalkan komentar

Aliran di antara dua plat

Aliran fluida di antara dua plat (gambar 1) merupakan kasus yang penting untuk ditinjau guna memahami sifat dasar pergerakan fluida. Hal ini dikatakan demikian karena setidaknya aliran di antara dua plat adalah contoh aliran internal dengan kondisi batas yang paling sederhana yaitu dengan geometri yang hanya mempunyai 2 dimensi karena menggunakan asumsi bahwa perubahan aliran pada dimensi ketiga dapat diabaikan. Dimensi ketiga diabaikan untuk menyederhanakan kasus agar proses pemahaman konsep dasar pergerakan fluida dapat dipahami dengan mudah, juga dikarenakan pergerakan fluida dua dimensi di antara dua plat datar sudah menjelaskan konsep fluida yang paling penting untuk mempelajari pergerakan fluida yaitu bilangan Reynold (Gambar 2).

Gambar 1. Aliran di antara 2 plat datar

Gambar 2. Bilangan Re.

Dapat diperhatikan pada gambar 2 di atas, bahwa bilangan reynold yang merepresentasikan turbulensi suatu aliran dipengaruhi oleh kerapatan (rho), kecepatan (v), viskositas dinamik fluida (mu), dan dimensi kondisi batas aliran (D). Dimana hubungan gradien kecepatan  terhadap arah y (laju regangan geser) dengan tegangan dan viskositas dinamik dapat diperhatikan pada gambar 3.

Gambar 3. Tegangan Geser

Dapat diperhatikan pada gambar 3 bahwa tegangan geser yang terdapat pada bagian plat yang berbatasan dengan batas aliran fluida tergantung terhadap viskositas fluida itu sendiri beserta profil alirannya (du/dy). Oleh karena itu, profil aliran fluida diperlukan untuk melihat perkembangan pergerakan fluida di dalam sebuah kondisi batas. Oleh karena itu akan diperlihatkan hasil dari simulasi yang telah dilakukan dimana hasil yang akan ditampilkan adalah perkembangan profil kecepatan fluida pada daerah “entrance region” (gambar 1) beserta kontur dari kecepatan itu sendiri di dalam wilayah komputasi dalam simulasi yang telah dilakukan.

Parameter – parameter yang ditetapkan dalam simulasi adalah sebagai berikut:

– Panjang = 5 m

– Tinggi = 0.5 m

– Resolusi sel dalam arah x (panjang) = 50

– Resolusi sel dalam arah y (tinggi) = 50

– Kerapatan fluida (rho) = 1E03 kg/m^3

Dengan variasi simulasi yang telah dilakukan adalah sebagai berikut

– case 1 : v = 0.5 m/s ; viskositas dinamik (mu) = 1 kg/m.s

– case 2 : v = 0.5 m/s ; viskositas dinamik (mu) = 10 kg/m.s

– case 3 : v = 1 m/s ; viskositas dinamik (mu) = 1 kg/m.s

– case 4 : v = 1 m/s ; viskositas dinamik (mu) = 10 kg/m.s

Dengan mengamati variasi – variasi di atas, dapat diambil perbandingan – perbandingan dari profil kecepatan pada kecepatan dan viskositas dinamik yang berbeda. Dimana dari case 1 dan case 2 serta case 3 dan case 4, profil kecepatan dapat dibandingkan dengan adanya perbedaan dari nilai viskositas dinamik. Kemudian dari case 1 dan case 3 serta case 2 dan case 4, perbedaan dari profil kecepatan dapat dibandingkan dimana perbedaan ini dihasilkan oleh adanya perubahan dari nilai kecepatan masuk dari fluida. Hal ini dapat diperhatikan dengan lebih jelas pada gambar 4.

Gambar 4. Relasi antara variasi parameter fisik simulasi

Pengaruh viskositas dinamik terhadap profil aliran

Berdasarkan persamaan Reynold, viskositas berpengaruh terhadap profil atau bentuk dari pergerakan fluida dimana pengaruhnya adalah berbanding terbalik (jika viskositas dinamik bertambah besar maka reynold akan semakin kecil yang mengartikan bahwa pergerakan fluida akan semakin laminer dan sebaliknya). Dapat diperhatikan pada gambar 5 dan gambar 6, kontur kecepatan fluida pada viskositas dinamik, masing – masing, sebesar 1 kg/m.s dan 10 kg/m.s.

Gambar 5. Profil kecepatan case 1

Gambar 6. Profil Kecepatan case 2

Secara visual, dapat diperhatikan perbedaan kontur pada profil kecepatan antara case 1 dan case 2. Pada case 2, dengan viskositas dinamik sebesar 10 kg/m.s, kontur kecepatan lebih dekat untuk menuju kondisi “fully developed” (gambar 1) dibandingkan case 1 yang memiliki viskositas 10 kali lipat lebih kecil dibandingkan dengan viskositas dinamik pada case 2. Dimana kondisi “fully developed” adalah kondisi dimana fluida memiliki kontur kecepatan yang sama di setiap koordinat x, relatif terhadap koordinat y.

Hal ini dapat dimengerti dengan memperhatikan wilayah yang mempunyai kecepatan yang kecil (warna biru). Dikarenakan kondisi viskositas dinamik pada case 2 yang relatif lebih besar terhadap case 1, maka wilayah biru ini lebih besar pada case 2 dibandingkan pada case 1. Hal ini dikarenakan oleh fluida pada case 2 yang memiliki kekentalan yang lebih besar dibandingkan dengan kekentalan fluida pada case 1. Oleh karena itu, fluida pada case 2 relatif lebih dekat, terhadap fluida pada case 1, untuk berada pada kondisi “fully developed” dikarenakan kekentalannya yang lebih besar. Hal ini dapat dikaitkan dengan persamaan bilangan Reynold pada gambar 2. Dengan memasukkan parameter – parameter pada case 1 dan 2, didapatkan nilai bilangan reynold pada case 1 dan 2, secara berurutan, adalah sebesar 240 dan 24. Dikarenakan kondisi bilangan reynold pada case 2 yang jauh lebih kecil dibandingkan dengan bilangan reynold pada case 1 maka dapat diambil kesimpulan bahwa aliran fluida pada case 1 lebih dekat untuk mencapai kondisi stabilnya/”fully developed”.

Perbandingan profil kecepatan antara case 3 dan 4 yang juga merupakan pengamatan terhadap pengaruh viskositas dinamik dapat diperhatikan pada gambar 7 dan gambar 8. Kesimpulan yang dapat dihasilkan dari perbandingan antara case 3 dan 4 adalah sama dengan case 1 dan 2, yang berbeda hanya variabel kecepatannya saja. Dimana pada case 1 dan 2, kecepatan adalah sebesar 0.5 m/s. Sedangkan pada case 3 dan 4, kecepatan adalah sebesar 1 m/s. Dengan bilangan Reynold pada case 3 dan 4, masing – masing, adalah sebesar 480 dan 48.

Gambar 7. Profil Kecepatan case 3

Gambar 8. Profil kecepatan case 4

Pengaruh kecepatan aliran terhadap profil aliran

Kecepatan aliran berdasarkan persamaan bilangan reynold berbanding lurus mempengaruhi parameter turbulensi aliran. Namun dikarenakan variasi kecepatan yang kecil pada simulasi, antara 0.5 m/s dan 1 m/s, yang hanya 2 kali. Tentunya sangat kecil dibandingkan dengan variasi terhadap viskositas dinamik yang 10 kali lipat. Dengan demikian, perbedaan aliran tidak begitu terlihat pada perbandingan dengan variasi kecepatan (case 1 dan case 3, case 2 dan case 4), khusus untuk simulasi ini.

Perbandingan dapat dilakukan dengan memperhatikan gambar 5 dan 7 (perbandingan case 1 dan case 3) serta gambar 6 dan 8 (perbandingan case 2 dan case 4). Jika diperhatikan dengan seksama, perbedaan tentu terlihat dengan case 1 lebih dekat untuk mencapai kondisi “fully developed” dibandingkan dengan case 3. Begitu juga dengan case 2 yang lebih dekat untuk mencapai kondisi “fully developed” dibandingkan dengan case 4. Hal ini berhubungan dengan perbandingan antara nilai reynoldnya yang dengan lebih jelas dapat diperhatikan pada tabel di bawah ini.

Tabel 1. Bilangan reynold untuk setiap case

Dari pembahasan sejauh ini, kesimpulan sementara yang dapat diambil adalah semakin besar bilangan reynold, maka semakin jauh untuk suatu fluida tersebut untuk berada pada kondisi stabilnya (“fully developed”). Hal ini dapat diperhatikan dengan mengurutkan Gambar profil kecepatan berdasarkan urutan bilangan reynoldnya yang secara berurutan adalah case 2 –> case 4 –> case 1 –> case 3. Hal ini dapat diperhatikan dengan lebih jelas pada gambar 9 sampai gambar 12.

Gambar 9. Profil kecepatan case 2

Gambar 10. Profil kecepatan case 4

Gambar 11. Profil Kecepatan case 1

Gambar 12. Profil kecepatan case 3

Sedangkan perkembangan profil kecepatan pada 70 cm pertama untuk setiap case, berurutan berdasarkan besarnya bilangan reynold, dapat diperhatikan pada gambar 13 sampai gambar 16 (grafik merah pada x = 0 m dan secara berurutan sampai grafik biru tua pada x = 0.7 m).

Gambar 13. Boundary layer development pada case 2

Gambar 14. Boundary layer development pada case 4

Gambar 15. Boundary layer development pada case 1

Gambar 16. Boundary layer development pada case 3

Dari gambar 13 sampai gambar 16, dapat diambil kesimpulan yang juga sama dengan pengamatan pada gambar  9 sampai gambar 12. Dapat diperhatikan pada gambar 13 bahwa pada x = 70 cm, kecepatan fluida sudah berada dalam bentuk stabilnya/”fully developed” (bentuk “fully developed” pada aliran diantara 2 plat dapat diperhatikan seperti pada bentuk “fully developed” pada gambar 1). Sedangkan pada gambar 16, dengan bilangan reynold sebesar 480, dapat diperhatikan bahwa fluida belum mencapai bentuk “fully developed”-nya pada x = 70 cm.

Kesimpulan yang dapat diambil dari pembahasan di atas adalah, semakin besar bilangan reynold maka semakin jauh untuk suatu fluida berada pada kondisi atau bentuk profil kecepatan stabilnya (“fully developed”).

2012
05/09
CATEGORY
Computational Fluid Dynamic
TAGS








Tinggalkan komentar

Ujian Tengah Semester CFD no. 2e

Analisa Hasil Simulasi Soal no. 2e. Ujian Tengah Semester

Mata Kuliah “Aplikasi CFD”

Dari penurunan persamaan konservasi momentum, diperoleh persamaan seperti berikut:

Persamaan 1 dan 2

yang berlaku untuk aliran di antara dua plat sejajar (aliran pada bidang dua dimensi) pada kondisi:

  1. Aliran tunak
  2. Arah aliran fluida hanya terdapat pada arah x (vektor kecepatan u)
  3. Tidak terdapat pembangkitan aliran, baik untuk vektor kecepatan u ataupun vektor kecepatan v

Dua persamaan atur di atas dapat diturunkan lagi menjadi sebagai berikut, yang dimana persamaan ini akan diverifikasi oleh simulasi yang akan dilakukan dengan mengklarifikasi nilai perbedaan tekanan ( ) pada rentang nilai x ( ) tertentu pada suatu koordinat sumbuy.

Persamaan 3

Dengan menetapkan nilai viskositas dinamik ( ) adalah konstan, yang sebesar 1 kg/ms, serta jarak antara dua plat (h) yang sebesar 0.48 m.

Gambar 1

Dapat diperhatikan pada gambar di atas, draft set – up simulasi yang akan dilakukan dengan L (x) adalah 5 m . Jadi, akan dilakukan simulasi aliran pada dua plat sejajar pada kondisi tunak dengan menetapkan perbedaan tekanan untuk setiap ujungnya.

Dalam menetapkan perbedaan tekanan, dengan asumsi  konstan sebesar 1 kg/ms dan h sebesar 0.48 m, maka persamaan 3 dapat dirubah menjadi,

Persamaan 4

Jadi, dengan  sebesar 5 m, maka  haruslah sebesar -260,42 Pa.

Jika diinginkan aliran mengalir dari kiri ke kanan (PA à PB), maka PA > PB. Maka,

 

Persamaan 5

Dengan menetapkan PB sebesar 101,325 kPa, maka besar nilai PA, untuk menghasilkan aliran laminar – tunak dengan arah aliran hanya pada arah kecepatan vector u tanpa adanya olakan dan pembalikan arah kecepatan, haruslah sebesar 101,58542 kPa.

Pada akhir simulasi, diperoleh distribusi nilai tekanan pada setiap kontrol volume skalar yang dari nilai ini dapat dilakukan verifikasi persamaan 3 dengan mengambil dua nilai tekanan pada interval jarak x tertentu pada suatu koordinat y. Dapat diperhatikan pada gambar 2, 3, dan 4 disttribusi grid pada simulasi (cell i = 0.05dan cell j = 0.01), profil kecepatan, dan profil tekanan total relative.

Gambar 2. Distribusi grid pada simulasi

Gambar 3. Profil kecepatan u (m/s)

Gambar 4. Profil tekanan total relatif

Dapat diperhatikan pada gambar 5 dan 6, nilai tekanan total relative untuk x = 0.025 m dan x = 2.5 m. Dapat diperhatikan pada gambar 6, nilai tekanan pada x = 2.5 m dan y = 2.4 m adalah sebesar 1.015E05 Pa.

Gambar 5. Distribusi tekanan pada x = 0.025 m

Gambar 6. Distribusi tekanan pada x = 2.5 m

Dengan melalui metode analitis, melalui persamaan 4 pada h = 0.24 m, nilai tekanan pada x = 2.5 m dan y = 2.4 m yang adalah sebesar 1.015E05 Pa dapat dievaluasi. Dengan menggunakan besar nilai P1 pada x = 0.025 m dan y = 0.24 m yang adalah sebesar 1.016E05 Pa, maka nilai P2 melalui metode analitis adalah sebagai berikut,

Dari hasil di atas, dapat diperhatikan bahwa antara metode analitis dan simulasi, didapat error yang sangat kecil, yang dimana ini dapat diakibatkan oleh pembagian grid yang kurang optimal. Namun, tetap kiranya besarnya error tersebut masih dapat ditoleransi, dengan error adalah sebagai berikut.

2012
05/09
CATEGORY
Computational Fluid Dynamic
TAGS



Tinggalkan komentar

Vortex Shedding

Pola aliran yang terbentuk akibat adanya benda penghalang (bluff body) sangat dipengaruhi oleh bilangan reynold yang menyatakan parameter aliran suatu fluida (Gambar 1). Dimana bilangan reynold ini bergantung terhadap kerapatan fluida, dimensi lintasan fluida, kecepatan fluida, dan viskositas dinamiknya. Pada saat bilangan reynold < 5, maka akan terjadi pola aliran yang halus atau tidak terjadi pembalikan arah aliran/pemisahan aliran pada boundary layer [1]. Dapat diperhatikan pada gambar 2, bahwa pola aliran yang terbentuk pada bilangan reynold < 5, tidak terdapat suatu fenomena dimana boundary layer terpecah/terpisah. Pada gambar 2, hanya terdapat laminar boundary layer dan turbulent boundary layer tanpa adanya vortex (pusaran lokal) pada pola aliran yang terbentuk.

Gambar 1. Persamaan Bilangan Reynold

Gambar 2. Pola aliran pada Re < 5

Sedangkan pada aliran yang mempunyai bilangan reynold diantara 5 dan 40 (5<Re<40), pemisahan pada boundary layer akibat meningkatnya gradien tekanan boundary layer (dp/dy) yang menyebabkan gradien kecepatan boundary layer (du/dy) menjadi nol dan mulai berbalik arah mulai terlihat (gambar 3). Hal ini menyebabkan adanya pusaran – pusaran lokal yang terbentuk pada pola aliran dibelakang benda penghalang (gambar 4). Namun dikarenakan bialngan reynoldnya yang belum terlalu besar, maka vortex yang terbentuk tidak sampai terpisah dari boundary layer pada bluff body.

Gambar 3. Pembentukan pusaran lokal pada boundary layer.

Gambar 4. Pola aliran di belakang benda penghalang pada saat 5<Re<40

Pada saat bilangan Reynold lebih dari 40 (Re>40), mekanisme pelepasan vortex (Vortex shedding) mulai terjadi. Hal ini dapat dijelaskan dengan mengamati gambar 5 dan gambar 6. Terlihat pada gambar 5 bagaimana mekanisme pelepasan/pemisahan vortex dari boundary layer terjadi. Jadi, karena pergerakan vortex B yang berlawanan arah jarum jam, maka vortex A yang bergerak searah dari jarum jam terpotong dan terlepas dari boundary layernya dimana hal ini disebabkan oleh pergerakan vortex B pada bilangan reynold yang relatif cukup besar (>40) untuk terjadinya mekanisme pemisahan vortex. Gambar 6 menunjukkan mekanisme serupa dengan gambar 5 namun dengan vortex C yang memotong vortex B atau vortex dari boundary layer bagian atas yang memotong vortex dari boundary layer bagian bawah. Dapat diperhatikan pada gambar 7 hasil simulasi vortex shedding dari I Giosan P. Eng [2].

Gambar 5. Vortex Shedding

Gambar 6. Vortex Shedding

Gambar 7. Hasil Simulasi Vortex Shedding pada [2]

Dengan demikian, penulis mencoba untuk mensimulasikan fenomena vortex shedding dengan menggunakan software CFDSOF. kerapatan, viskositas, panjang wadah aliran, dan lebar wadah aliran adalah masing – masing 1000 kg/m^3, 1E-5 kg/ms, 1 m, dan 4.8E-1 m. Dengan banyaknya cell/mesh/grid pada arah x dan y adalah 50. Berikut hasil simulasi dalam bentuk video.

Sekian kiranya yang penulis dapat disampaikan saat ini. Semoga bermanfaat.

Wassalam.

Referensi:

[1] http://rudiwp.files.wordpress.com/2006/11/apa-itu-vortex-shedding.pdf. 3 Mei 2012. 17.00 WIB

[2] I. Giosan, P.Eng. Vortex Shedding Induced Loads on Free Standing Structures. Structural Vortex Shedding Response Estimation Methodology and Finite Element Simulation

[3] SFPE. (2002). SFPE Handbook of Fire Protection Engineering, National Fire Protection Association (NFPA), Quincy, MA.

2012
05/08
CATEGORY
Computational Fluid Dynamic
TAGS




Tinggalkan komentar

Solusi Numerik beberapa Parameter Boundary Layer

Pada post kali ini, saya ingin mencoba untuk menyampaikan beberapa persamaan hasil pendekatan numerik terhadap penyelesaian solusi numerik beberapa parameter boundary layer seperti profil kecepatan, hambatan, profil temperatur, dan koefisien perpindahan panas. Untuk lebih jelasnya, berikut permasalahannya,

Agar lebih jelasnya, sepertinya perlu untuk pertama – tama dijelaskan mengenai fundamental penyelesaian dinamika fluida secara numerik, khususnya dengan menggunakan metode volume hingga.

Dalam menggunakan metode numerik volume hingga, wilayah komputasi dibagi menjadi beberapa bagian (cell/grid) untuk dengan kemudian pada cell/grid tersebut diaplikasikan hukum – hukum konservasi untuk mendapatkan solusi terhadap variabel/field tekanan, kecepatan (pada sumbu x, y, dan z), serta temperatur. Berikut persamaan – persamaan konservasi yang disebutkan di atas.

Pembagian grid – grid dilakukan secara tumpang tindih untuk mengaplikasikan perhitungan secara numerik, yang dapat diperhatikan pada gambar di bawah ini.

Dapat diperhatikan pada gambar di atas bahwa tanda panah yang merupakan variabel vektor, mempunyai kontrol volume yang tumpang tindih dengan P yang merupakan variabel skalar. Jadi, pada intinya, pembagian grid pada kalkulasi numerik dinamika fluida adalah pembagian grid yang tumpang tindih antara grid variabel skalar dan vektor.

Salah satu algoritma perhitungannya dapat dilakukan dengan metode SIMPLE yang ringkasnya adalah sebagai berikut.

Dimana persamaan – persamaan pada gambar di atas adalah persamaan – persamaan atur yang sudah didiskritisasi, khususnya dari persamaan konservasi momentum (STEP 1). Sedangkan pada Step 4 (langkah 4), persamaan diskrit tersebut berasal dari persamaan konservasi lainnya misal persamaan konservasi energi untuk mencari solusi terhadap profil temperatur.

Pada gambar di atas, variabel p, u, v, w, tetha, A,  merepresentasikan tekanan, kecepatan fluida pada sumbu x, kecepatan fluida pada sumbu y, kecepatan pada sumbu z, variabel – variabel diskrit lainnya, misal temperatur, dan luas penampang bidang i, J. Sedangkan variabel dengan lambang asterisk (*) merepresentasikan variabel dugaan awal untuk memulai perhitungan. Serta variabel dengan lambang ” ‘ ” merupakan faktor koreksi terhadap variabel dugaan awal. Dapat diperhatikan bahwa pada langkah 1, perhitungan dapat dilakukan dengan metode kalkulasi matriks seperti eliminasi gauss atau iterasi Gauss – Siedel.

Variabel – variabel lain seperti pada gambar di atas seperti ai,J ; Sigma(anb.unb); bi,J; dan beberapa variabel lain yang terdapat pada gambar algoritma di atas dapat diperhatikan lebih jelasnya pada gambar di bawah ini.

Sigma(anb.unb) untuk kontrol volume kecepatan vektor u

Sigma(anb.unb) untuk kontrol volume kecepatan vektor v

beberapa variabel lainnya,

dimana.

Dengan demikian, perhitungan numerik dapat dilakukan dengan mengaplikasikan persamaan – persamaan di atas, dengan menggunakan algoritma yang telah ditunjukkan.

Karena kapasitas blogger yang saat ini masih terbatas, khususnya untuk mengaplikasikan algoritma di atas dalam bentuk bahasa pemrograman, maka solusi numerik untuk permasalahan di atas diselesaikan dengan mengambil data dari hasil simulasi dengan menggunakan program CFDSOF. Kemudian untuk mengetahui profil kecepatan dan temperatur, data – data hasil dari simulasi dapat diambil dengan kemudian diplot grafiknya.

Berikut set – up simulasi yang dilakukan sebelumnya, dengan jumlah cell/grid pada arah x dan y, masing – masing adalah 50 dan 20.

Berikut beberapa data hasil simulasi untuk kecepatan u

Berikut bentuk profile kecepatannya untuk i = 2, i = 25, dan i = 49.

Sedangkan untuk mengetahui profile temperatur akibat adanya pembangkitan panas pada plat datar sebesar 1 kW/m(pangkat 2), dapat kembali diplot beberapa data dari hasil simulasi seperti di bawah ini,

Maka, berikut gambar profil boundary layer temperatur untuk i = 2, i = 5, dan i = 7

Sedangkan untuk melihat profile dari koefisien transfer konveksi, dapat dilihat dengan mem – plot data dari hasil simulasi seperti di bawah ini,

Serta berikut profil koefisien konveksi untuk i = 2, i = 5, dan i = 7

 

Referensi:

HK. Versteeg, Malalasekera W., An Introduction to Computational Fluid Dynamic : Chapter 6. Longman Scientific & Technical.1995.

2012
04/20
CATEGORY
Computational Fluid Dynamic
Komputasi Teknik
TAGS







1 komentar

Visualisasi Distribusi Temperatur pada Proses Perpindahan Panas Konduksi pada Batang Sederhana yang disertai dengan Pembangkitan Panas.

Pada post kali ini, saya ingin menampilkan hasil visualisasi yang tetap berkaitan dengan post saya sebelumnya mengenai proses perpindahan panas konduksi pada batang sederhana. Namun, perbedaan yang ingin saya tampilkan saat ini adalah visualisasi distribusi temperature yang diakibatkan oleh adanya pembangkitan panas pada batang sederhana yang disimulasikan. Pembangkitan panas pada simulasi ini ditetapkan sebesar 1000 kW/m3. Berikut ilustrasi kasus perpindahan panas yang akan disimulasikan.

   

Dengan asumsi dan konstanta yang sama dengan post sebelumnya, maka berikut visualisasi distribusi temperature pada batang sederhana yang disimulasikan.

 

 

Dapat diperhatikan pada gambar dan grafik di atas, bahwa dikarenakan oleh adanya pembangkitan panas sebesar 1000- kW per satuan volume, menyebabkan distribusi temperature meningkat jika dibandingkan dengan distribusi temperature pada batang sederhana tanpa pembangkitan panas.

Jika diperhatikan terlebih dahulu set – up geometri batang sederhana yang disimulasikan,

   

Dengan menetapkan perbedaan temperature dengan cara memberikan nilai 100oC pada W1 dan 500oC pada W2, maka W1 dan W2 berfungsi sebagai poin A dan poin B pada gambar pertama di atas. Maka distribusi temperature yang akan diperhatikan atau dihitung adalah temperature pada tiap – tiap batas diskrit volume W2. Dapat diperhatikan pada gambar di atas bahwa terdapat 6 batas diskrit volume W2, yang dimana hal ini sesuai dengan jumlah titik belok grafik beserta titik awal dan akhir. Jadi, dapat disimpulkan bahwa hasil pada grafik sangat terikat dengan pembagian diskrit volume pada simulasi. Jika seandainya diskrit volume diperbanyak lagi, maka akan semakin banyak pula titik belok yang terbentuk, sampai pada jumlah tertentu yang dapat mengilustraikan bentuk grafik kurva yang halus.

Sekian yang dapat saya sampaikan untuk saat ini. Semoga bermanfaat.

Wassalam.

Note: untuk detail perhitungan fundamental berdasarkan metode volume hingga mengenai kasus konduksi seperti pada gambar di atas, dapat dilihat pada Versteeg H.K., Malalasekera W. Introduction to computational fluid dynamics. The finite volume method (Longman, 1995)

2012
04/09
CATEGORY
Computational Fluid Dynamic
TAGS




Tinggalkan komentar

Visualisasi Distribusi Temperatur pada Batang Sederhana yang Mengalami Konduksi

Pada post kali ini, saya ingin menampilkan visualisasi distribusi temperature pada batang sederhana yang mengalami konduksi. Proses perpindahan panas secara konduksi yang terjadi pada batang yang akan disimulasikan disebabkan oleh adanya perbedaan temperature pada tiap – tiap ujung batang sederhana. Berikut ilustrasi batang sederhana yang akan disimulasikan

 

Pada gambar di atas, telah dijelaskan bahwa, proses perpindahan panas secara konduksi disebabkan oleh perbedaan temperature pada ujung A dan ujung B, dimana nilainya masing – masing adalah 100oC dan 500oC. Jadi dapat diprediksi bahwa arah perpindahan panas adalah dari arah kanan (B) ke kiri (A). Atau dengan kata lain, temperature akan semakin turun dari arah kanan ke kiri, dan sebaliknya.

Simulasi dijalankan dengan asumsi bahwa kondisi perpindahan panas sudah berada pada kondisi tunaknya dengan diskritisasi volume dalam arah vertical (sumbu i) sebanyak 7.

Note: untuk detail perhitungan fundamental berdasarkan metode volume hingga mengenai kasus konduksi seperti pada gambar di atas, dapat dilihat pada Versteeg H.K., Malalasekera W. Introduction to computational fluid dynamics. The finite volume method (Longman, 1995)

Dapat diperhatikan gambar di bawah ini yang merepresentasikan set – up geometri dua dimensi yang akan disimulasikan dengan menggunakan software CFDSOF. Jadi, ditetapkan W1 dan W2 sebagai, masing – masing, titik A dan B.

 

Dengan menetapkan nilai konduktivitas batang sebesar 100 W/mK, maka didapatkan distribusi temperature seperti pada gambar di bawah ini.

 

Dapat diperhatikan bahwa, pada kondisi tunaknya dengan temperature pada masing – masing ujung batang adalah sebesar 100oC dan 500oC, distribusi temperature merepresentasikan arah perpindahan kalor yang sesuai dengan ekspektasi awal, yaitu dari arah kanan ke kiri. Memang hal ini sudah kita ketahui bersama, namun poin penting yang perlu diambil dari simulasi ini adalah dapatnya kalkulasi untuk melihat distribusi temperature dengan perbedaan temperature tertentu dilakukan. Untuk dapat dengan lebih jelas melihat distribusi temperature dari hasil simulasi, dapat diperhatikan grafik di bawah ini.

 

Grafik di atas menunjukkan distribusi temperature berdasarkan arah sumbu i, yang jika diperhatikan dari kiri ke kanan adalah dari poin A ke poin B. Dapat diperhatikan bahwa temperature terdistribusi secara linear sepanjang sumbu i. Namun, hasil grafik ini hanya berlaku untuk penyelesaian masalah dengan diskritisasi volume sebanyak 7. Jika diskritisasi volume diperbanyak lagi, hasil akhir yang didapatkan dapat saja berbeda dengan grafik di atas.

 

Sekian yang dapat saya sampaikan saat ini. Semoga bermanfaat.

Wassalam

 

2012
04/09
CATEGORY
Computational Fluid Dynamic
TAGS


Tinggalkan komentar

Metode Volume Hingga pada proses difusi konveksi

Pada posting kali ini, saya ingin mencoba untuk menjelaskan secara ringkas mengenai penggunaan metode volume hingga (Finite Volume Method) pada kalkulasi numerik difusi dalam bentuk konveksi.

Jadi, sebelumnya, perlu untuk kita mengingat persamaan umum transport pada posting sebelumnya, https://muhammadagungsantoso.wordpress.com/2012/03/13/diskritisasi-persamaan-atur-dengan-metode-volume-hingga/, yang adalah

Untuk sekedar mengulang apa yang sudah disampaikan sebelumnya, bahwa suku pertama di sebelah kanan persamaan adalah suku yang berkaitan dengan keterikatan variabel yang sedang ditinjau dengan waktu. Jadi, jika variabel yang sedang ditinjau (misal, temperatur) tidak berubah – ubah berdasarkan temperatur, maka suku pertama dari persamaan ini dapat diasumsikan nol.

Sedangkan suku kedua di sebelah kanan pada persaman di atas adalah suku yang berkaitan dengan keluar dan masuknya variabel yang bersangkutan ke dalam suatu diskritisasi volume kontrol yang sedang ditinjau (misal momentum)

Untuk kondisi tunak, dimana variabel yang sedang ditinjau tidak berubah – ubah berdasarkan waktu, maka suku transien yang merupakan suku pertama di sebelah kiri persamaan di atas dapat dieliminasi sehingga bentuk persamaan umum menjadi,

Jadi, dengan suku sebelah kiri adalah suku aliran masuk dan keluar variabel phi terhadap diskritisasi volume, suku pertama di sebelah kanan persamaan adalah suku yang merepresentasikan difusifitas dari variabel phi, dan suku kedua di sebelah kanan adalah suku yang merepresentasikan pembangkitan suatu variabel phi di dalam diskritisasi volume, perhitungan dapat dilakukan dengan berbagai metode kalkulasi numerik yang misal adalah sebagai berikut:

1. The Central Differencing Scheme

2. The Upwind Differencing Scheme

3. The Hybrid Differencing Scheme

4. The Power Law Scheme

Kiranya hanya sekian yang dapat blogger sampaikan kali ini. Untuk penjelasan mengenai metode – metode kalkulasi numerik yang telah disebutkan di atas, mungkin akan di post pada kesempatan selanjutnya. Semoga. Amin

Semoga bermanfaat. Wassalam.

2012
03/20
CATEGORY
Computational Fluid Dynamic
TAGS




Tinggalkan komentar

Diskritisasi Persamaan Atur dengan Metode Volume Hingga

Beberapa persamaan atur yang digunakan dalam kalkulasi CFD adalah

– Persamaan Massa

– Persamaan Gaya

– Arah x

– Arah y

– Arah z

– Persamaan Energi

– Persamaan Keadaan

Untuk menyelesaikan persamaan – persamaan di atas, metode kalkulus yang ada tidak mencukupi. Oleh karena itu, metode numerik digunakan untuk memecahkan persamaan di atas.

Diskritisasi

Yang dimaksud dengan diskritisasi adalah memecah domain atau daerah perhitungan menjadi beberapa daerah – daerah kecil yang disebut dengan grid, mesh, atau cell. Dengan terlebih dahulu menetapkan nilai pada kondisi batas daerah perhitungan (Boundary Condition), maka nilai kecepatan aliran, tekanan, dan temperatur dapat dihitung pada tiap – tiap mesh/cell/grid yang sudah ditetapkan berdasarkan persamaan – persamaan atur di atas.

General Transport Equation

Persamaan – persamaan atur yang telah disebutkan di atas, dapat direpresentasikan dalam satu bentuk umumnya yang dapat diperhatikan seperti di bawah ini,

dengan,

Suku pertama pada sebelah kiri persamaan umum di atas merepresentasikan kondisi tunak atau tidak dari suatu kondisi tertentu. Jadi, jika kondisi tertentu (misal gaya atau massa) tidak berubah berdasarkan waktu (tunak), maka suku ini bernilai nol.

Sedangkan suku kedua pada sebelah kiri persamaan di atas berhubungan dengan keadaan konveksi dari suatu kondisi atur. Suku pertama pada sebelah kanan pada persamaan di atas adalah hubungan difusi suatu kondisi atur. Dan suku terakhir pada persamaan umum di atas adalah perubahan nilai variabel atur yang dikarenakan oleh sumber terhadap variabel atur yang terdapat di dalam daerah komputasi.

2012
03/13
CATEGORY
Computational Fluid Dynamic
TAGS






Tinggalkan komentar