Metoda Iterasi
Post kali ini, mengenai metode – metode iterasi yang sering digunakan pada metode numerik untuk kalkulasi solusi suatu persamaan atau sistem persamaan. Jadi, inti dari Iterasi adalah, menyelesaikan atau mencari solusi dari suatu persamaan atau sistem persamaan tertentu dengan:
– mengestimasi nilai awal salah satu variabel
– menentukan toleransi error untuk solusi akhir
– Memulai perhitungan pada persamaan atau sistem persamaan dengan algoritma metode iterative
– Kemudian mengulang lagi perhitungan dengan adanya variabel yang digantikan oleh variable baru hasil perhitungan dari perhitungan sebelumnya sesuai dengan kondisi algoritma metode iterative yang digunakan
– Perhitungan terus berulang hingga error dari variabel hasil perhitungan, relatif terhadap suatu variabel lainnya, mencapai nilai yang sudah ditetapkan
Pengulangan – pengulangan perhitungan yang terjadi, berdasarkan error, adalah yang disebut dengan iterasi, dan dilakukan terus sampai error mengecil, yang mengartikan bahwa nilai variabel solusi sudah mulai menuju satu titik (Konvergen)
Berikut beberapa metode iterative yang sering digunakan untuk mencari solusi dari persamaan atau sistem persamaan:
1. Metode Bisection
2. Metode “False Position”
3. Metode Newton – Raphson
4. Metode Secant
5. Metode Aproksimasi “Succesive”
Berikut sedikit penjelasan mengenai metode – metode iterative yang disebutkan di atas:
1. Metode Bisection
Metode bisection merupakan metode yang digunakan untuk mencari solusi dari persamaan tertentu. Filosofi yang digunakan pada metode bisection adalah memperkecil rentang nilai variabel bebas yang di dalamnya terdapat solusi ingin dicari. Jadi, seni yang terdapat pada metode bisection ini adalah mencari rentangan nilai variabel bebas yang di dalamnya terdapat solusi yang diinginkan. Mungkin dapat diperhatikan pada gambar di bawah ini untuk lebih jelasnya.
Jadi, pada gambar di atas, dapat diperhatikan bahwa untuk menemukan solusi persamaan (akar persamaan), yang sesuai dengan persamaan yang ditunjukkan pada grafik tersebut, dipilih dua nilai a dan b yang merupakan nilai dari sumbu x. Salah satu ketetapan yang perlu untuk dijelaskan terlebih dahulu pada metode Bisection adalah, pada perkiraan nilai yang akan menjadi interval estimasi penentuan solusi akar persamaan (pada kasus gambar di atas, merupakan nilai a dan b), perlu agar nilai a dan b untuk menghasilkan nilai persamaan (f(a) dan f(b)) yang mempunyai tanda yang berlainan (+ atau -).
Setelah interval awal ditetapkan, maka iterasi dengan metode bisection dapat dilakukan, hal ini dilakukan dengan pertama – tama menentukan nilai x (pada gambar di atas, merupakan nilai x1) di tengah – tengah nilai a dan b. Setelah itu, dicari nilai persamaan untuk terhadap nilai x dan nilai a (f(x) dan f(a)). Kemudian, jika tanda pada nilai persamaan f(x) dan f(a) sama, maka pada kalkulasi berikutnya, x1 akan berperan menjadi a pada perhitungan selanjutnya. Namun, jika tidak, maka nilai x1 akan berperan sebagai nilai b pada perhitungan selanjutnya.
Selanjutnya kalkulasi dihitung kembali dengan interval baru yang dimana salah satu dari nilai intervalnya digantikan oleh nilai x1, sesuai dengan ketetapan tanda pada nilai persamaan di perhitungan sebelumnya. Setelah itu, dicari kembali nilai tengah antara interval yang baru, dan perhitungan diulang lagi (iterasi) sampai pada tingkat keakuratan tertentu (e). Dimana e < (b – a)/b. Untuk lebih jelasnya, dapat diperhatikan gambar di bawah ini yang mengilustrasikan langkah iterative pada metode Bisection, atau dengan memperhatikan posting saya sebelumnya, Metoda Iterative Bisection dalam kalkulasi solusi persamaan polynomial orde tiga.
2. Metode “False Position”
Metode “false position” merupakan improvisasi dari metode Bisection. Jadi, pada metode “false position” tetap digunakan dua nilai interval (misal a dan b) di antara nilai solusi akar persamaan yang memiliki tanda berlainan pada masing – masing nilai persamaannya. Namun, yang berbeda dari iterasi “false position” dengan metode Bisection adalah pencarian nilai diantara interval pertama yang dicari dengan menarik garis lurus antara f(a) dan f(b) dan mengambil nilai x1 (nilai di antara a dan b) dari perpotongan garis f(a) -> f(b) dengan sumbu x. Jadi, dibandingkan dengan mengambil nilai x1 sebagai pertengahan nilai a dan b pada metode bisection, algoritma pada metode “false position” dapat diartikan memiliki jumlah pengulangan perhitungan yang lebih kecil (cepat) dibandingkan metode bisection karena dengan mengambil nilai x1 sebagai perpotongan garis f(a) -> f(b), maka nilai x1 lebih mendekati solusi akar persamaan dibandingkan metode bisection. Lebih jelasnya, dapat diperhatikan pada gambar di bawah ini (dengan berikut variabel – variabel pada gambar yang relevan dengan variabel – variabel pada penjelasan paragraf di atas, a = z1, b = z2, x1 = zs, f(x) = g(z), f(a) = g(z1), f(b) = g(z2), f(x1) = g(zs).
Persamaan untuk menentukan nilai zs (sesuai dengan gambar di atas) dapat diturunkan dari persamaan tangensial sudut. Singkatnya, nilai zs dapat ditentukan sesuai dengan persamaan sebagai berikut.
kemudian, dicari nilai fungsi persamaan berdasarkan nilai zs. Jika masih diluar toleransi keakuratan, maka kalkulasi diulang kembali (iterasi) dengan mengganti salah satu nilai z1 atau z2 dengan nilai zs sesuai dengan ketetapan tanda nilai fungsi z1 dan zs. Jadi, jika tanda g(z1) sama dengan tanda g(zs), maka nilai z1 pada perhitungan selanjutnya digantikan dengan nilai zs, namun jika tidak, maka z2 yang digantikan oleh zs. Jadi, perhitungan tetap beriterasi selama g(zs) belum mendekati nilai 0, tentunya sesuai dengan toleransi keakuratan yang sudah ditetapkan.
3. Metode Newton – Raphson
Metode Iterasi Newton – Raphson merupakan metode yang benar – benar berlainan dengan metode – metode iterasi sebelumnya yang sudah dijelaskan. Untuk lebih jelasnya, perlu untuk pertama – tama memperhatikan gambar di bawah ini.
Jadi, dipilih suatu nilai estimasi xo sembarang. Kemudian ditentukan titik x1 yang merupakan antara perpotongan garis singgung f(x0) dengan sumbu x. Dimana kemiringan garis singgung f(x0) adalah f'(x0). Persamaan untuk mendapatkan nilai x1 dapat diperoleh dengan meninjau persamaan tangensial sudut antara garis singgung f(x0) dengan sumbu x, yang adalah
yang sederhananya adalah sebagai berikut
Kemudian, kalkulasi diulang kembali dengan menggati nilai x0 dengan x1 untuk mencari nilai x2. Berikut bentuk umum persamaan di atas,
Jadi, perhitungan terus beriterasi sampai pada nilai f(x(i+1)) atau selisih antara xi dan x(i+1) mendekati nol atau sesuai dengan tingkat tolerasi keakuratan yang diinginkan. Dari algoritma perhitungan yang dijelaskan ataupun dari gambar ilustrasi metode newton – raphson di atas , dapat kita ambil kesimpulan bahwa iterasi pada metode Newton – Raphson jauh lebih cepat dibandingkan dengan iterasi pada metode Bisection dan “False Position”. Namun, kekurangan yang dimiliki oleh metode Newton – Raphson adalah perlunya ketepatan dalam pemilihan nilai estimasi awal, yang dengan demikian menyebabkan tidak terjaminnya konvergensi pada metode newton – Raphson. Untuk lebih mudahnya, dapat diperhatikan salah satu contoh divergensi pada gambar di bawah ini.
Gambar di atas mengilustrasikan salahnya estimasi nilai awal pada kalkulasi newton – raphson. Jadi, dengan menetapkan estimasi nilai x0 seperti pada gambar di atas, berakibat kepada kemiringan garis singgung yang nilainya mendekati nol (f'(x2) mendekati nol). Jadi, dapat juga dilihat pada persamaan umum newton – raphson di atas, yang perhitungannya memerlukan ketetapan awal yang dimana f'(xi) tidak boleh sama dengan nol atau mendekati nol. Karena, sesuai peninjauan grafis, jika kemiringan garis singgung fungsi sama dengan nol, maka garis singgung tidak akan pernah memotong sumbu x yang berakibat tidak diperolehnya estimasi lanjutan nilai x.
4. Metode Secant
Metode secant adalah metode yang menyederhanakan perhitungan yang akan dilakukan, relatif terhadap metode Newton – Rephson. Penyederhanaan yang dilakukan adalah dengan mengeliminasi kalkulasi f'(x) pada algoritma. Hal ini dikarenakan, sering suatu bentuk persamaan tertentu mempunyai bentuk persamaan yang kompleks, rumit, dan panjang sehingga memerlukan waktu komputasi yang lebih lama.
Pada metode iterative secant, diperlukan dua nilai estimasi awal, yang dimana nilai ini tidak perlu merupakan interval yang di dalamnya terdapat solusi akar persamaan. Jadi, jika merujuk dari gambar di atas, dengan z1 dan z2 adalah merupakan dua nilai estimasi awal, ditarik garis secant antara g(z1) dan g(z2). Perpotongan antara garis secant tersebut dengan sumbu x, menghasilkan nilai zs(1). Selanjutnya, ditarik kembali garis secant antara g(z2) dan g(zs(1)) yang akan berpotongan dengan sumbu x di zs(2). Kemudian berlanjut lagi dengan menarik garis secant antara g(zs(1)) dan g(zs(2)) yang akan berpotongan di nilai zs selanjutnya. Begitu seterusnya hingga nilai g(z) mendekati nol sesuai dengan toleransi keakuratan yang telah ditetapkan sebelumnya. Namun, estimasi nilai awal tetap merupakan faktor penting dalam konvergensitas iterasi. Oleh karena itu, sama halnya dengan metode newton – raphson, metode secant tidak menjamin suatu konvergensitas iterasi di semua nilai estimasi awal solusi.
Persamaan berikut ini, yang diturunkan dari persamaan tangensial dapat diperhatikan seperti berikut.
dengan g'(z2) dikalkulasi sesuai dengan perhitungan berikut.
setelah subtitusi persamaan g'(z) ke dalam persamaan zs(1) dan menyederhanakannya, diperoleh persamaan sebagai berikut.
Jadi, dari penjelasan di atas, ketidak – ikutsertaan kalkulasi derivasi dari fungsi persamaan yang ingin dicari solusinya, menyebabkan metode secan mempunyai waktu iterasi yang relatif lebih cepat dibandingkan metode Newton – Raphson. Namun, sama halnya juga dengan metode Newton – Raphson, metode secant tidak menjamin suatu konvergensitas iterasi di semua nilai estimasi awal solusi.
5. Metode Aproksimasi “Successive”
Metode aproksimasi suksesive adalah metode iterasi yang sangat mudah untuk diprogram di komputer. Jadi, inti dari algoritma metode iterasi ini adalah merubah bentuk dari suatu fungsi f(x) = 0 menjadi x = g(x). Dengan membayangkan bahwa terdapat garis y = x dan y = g(x), maka solusi akar persamaan untuk f(x) terletak pada perpotongan garis y = x dan kurva y = g(x). Berikut ilustrasinya,
Dimana yang dimaksud dengan phi(x) pada gambar di atas adalah g(x). Jadi, secara umum,
x1 = g(x0), x2 = g(x1), …, x( i+1) = g(xi), …, xn = g(x(n-1))
Jadi solusi akan diperoleh pada saat interval relative xi dan x(i+1) atau g(i) dan g(i+1) berada pada toleransi keakuratan yang sudah ditetapkan sebelumnya.





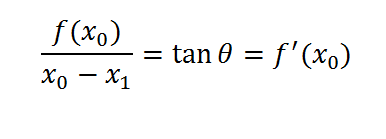








yang paling bagus dan cepat dengan error sama dan jumlah iterasi sama, kira-kira metode mana ya?
metode ini tentunya punya kelebihan dan kelemahan.. yang paling praktis yang mana ya gung?
terima kasih
Yup pertanyaan saya hampir sama dengan mas hasnan.Saya maunya kapan dan atas pertimbangan apa kita harus memilih salah satu diantara banyak metode iterative yang akan kita gunakan untuk menyelesaikan kasus yang sedang kita ingin selesaikan??
salam,
arandityonarutomo.blogspot.com
Apakah dengan iterasi yang sama hasil juga akan mendekati sama tiap metode bung agung
Mas mas, mau tanya..
Itu kelebihan dan kekurangan dari tiap metode apa ya?
terima kasih..
penjelasan yang sangat menarik. Alangkah baiknya jika dibuat model chart ato tabel untuk lebih memudahkan dalam mengerti kelebihan dan kekurangan masing-masing metode.
Menarik sekali penjelasan dari Agung. Seperti komentar Ragil, perlu dilengkapi kelebihan dan kekurangan masing-masing metode agar pembaca lebih paham dan bisa memilih metode yang tepat untuk kasus-kasus tertentu.
visit my blog
mhs.blog.ui.ac.id/daniel81
gung metode mana aja yang uda dicoba?
Wah, master matematik kalo udah berbicara ngeri nih.haha